Trigonometry

The study of angles and the angular relationships of planar and three-dimensional figures is known as trigonometry. The trigonometric functions (also called the circular functions) comprising trigonometry are the cosecant , cosine , cotangent , secant , sine , and tangent . The inverses of these functions are denoted , , , , , and . Note that the notation here means inverse function, not to the power.

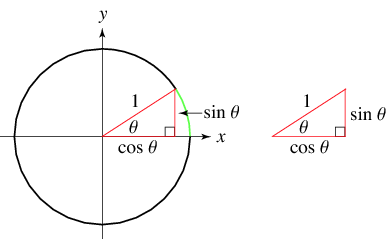
The trigonometric functions are most simply defined using the unit circle. Let be an angle measured counterclockwise from the x-axis along an arc of the circle. Then is the horizontal coordinate of the arc endpoint, and is the vertical component. The ratio is defined as . As a result of this definition, the trigonometric functions are periodic with period , so

(1)

where is an integer and func is a trigonometric function.

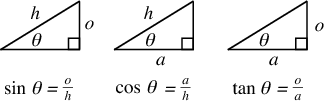
A right triangle has three sides, which can be uniquely identified as the hypotenuse, adjacent to a given angle , or opposite . A helpful mnemonic for remembering the definitions of the trigonometric functions is then given by "oh, ah, o-a," "Soh, Cah, Toa," or "SOHCAHTOA", i.e., sine equals opposite over hypotenuse, cosine equals adjacent over hypotenuse, and tangent equals opposite over adjacent,

			(2)
			(3)
			(4)

Another mnemonic probably more common in Great Britain than the United States is "Tommy On A Ship Of His Caught A Herring."

From the Pythagorean theorem,

(5)

It is therefore also true that

(6)

and

(7)

The trigonometric functions can be defined algebraically in terms of complex exponentials (i.e., using the Euler formula) as

			(8)
			(9)
			(10)
			(11)
			(12)
			(13)
			(14)
			(15)
			(16)
			(17)
			(18)

Hybrid trigonometric product/sum formulas are

			(19)
			(20)
			(21)
			(22)

Osborne's rule gives a prescription for converting trigonometric identities to analogous identities for hyperbolic functions.

For imaginary arguments,

			(23)
			(24)

For complex arguments,

			(25)
			(26)

For the absolute square of complex arguments ,

			(27)
			(28)

The complex modulus also satisfies the curious identity

(29)

The only functions satisfying identities of this form,

(30)

are , , and (Robinson 1957).