In antiquity, geometric constructions of figures and lengths were restricted to the use of only a straightedge and compass (or in Plato's case, a compass only; a technique now called a Mascheroni construction). Although the term "ruler" is sometimes used instead of "straightedge," the Greek prescription prohibited markings that could be used to make measurements. Furthermore, the "compass" could not even be used to mark off distances by setting it and then "walking" it along, so the compass had to be considered to automatically collapse when not in the process of drawing a circle.
Because of the prominent place Greek geometric constructions held in Euclid's Elements, these constructions are sometimes also known as Euclidean constructions. Such constructions lay at the heart of the geometric problems of antiquity of circle squaring, cube duplication, and angle trisection. The Greeks were unable to solve these problems, but it was not until hundreds of years later that the problems were proved to be actually impossible under the limitations imposed. In 1796, Gauss proved that the number of sides of constructible polygons had to be of a certain form involving Fermat primes, corresponding to the so-called Trigonometry Angles.
Although constructions for the regular triangle, square, pentagon, and their derivatives had been given by Euclid, constructions based on the Fermat primes 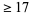 =17" border="0" width="30" height="14"> were unknown to the ancients. The first explicit construction of a heptadecagon (17-gon) was given by Erchinger in about 1800. Richelot and Schwendenwein found constructions for the 257-gon in 1832, and Hermes spent 10 years on the construction of the 65537-gon at Göttingen around 1900 (Coxeter 1969). Constructions for the equilateral triangle and square are trivial (top figures below). Elegant constructions for the pentagon and heptadecagon are due to Richmond (1893) (bottom figures below).
=17" border="0" width="30" height="14"> were unknown to the ancients. The first explicit construction of a heptadecagon (17-gon) was given by Erchinger in about 1800. Richelot and Schwendenwein found constructions for the 257-gon in 1832, and Hermes spent 10 years on the construction of the 65537-gon at Göttingen around 1900 (Coxeter 1969). Constructions for the equilateral triangle and square are trivial (top figures below). Elegant constructions for the pentagon and heptadecagon are due to Richmond (1893) (bottom figures below).
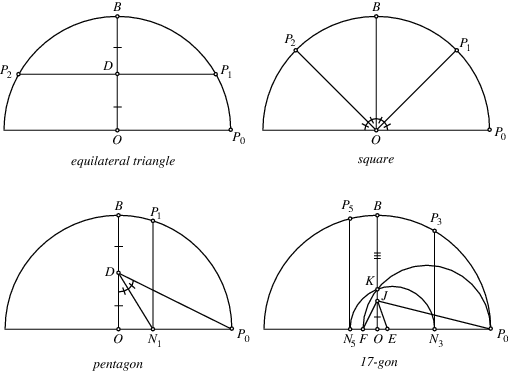
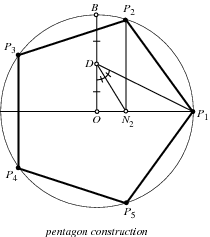
Given a point, a circle may be constructed of any desired radius, and a diameter drawn through the center. Call the center ![]() , and the right end of the diameter
, and the right end of the diameter ![]() . The diameter perpendicular to the original diameter may be constructed by finding the perpendicular bisector. Call the upper endpoint of this perpendicular diameter
. The diameter perpendicular to the original diameter may be constructed by finding the perpendicular bisector. Call the upper endpoint of this perpendicular diameter ![]() . For the pentagon, find the midpoint of
. For the pentagon, find the midpoint of ![]() and call it
and call it ![]() . Draw
. Draw ![]() , and bisect
, and bisect ![]() , calling the intersection point with
, calling the intersection point with ![]()
![]() . Draw
. Draw ![]() parallel to
parallel to ![]() , and the first two points of the pentagon are
, and the first two points of the pentagon are ![]() and
and ![]() . The construction for the heptadecagon is more complicated, but can be accomplished in 17 relatively simple steps. The construction problem has now been automated (Bishop 1978).
. The construction for the heptadecagon is more complicated, but can be accomplished in 17 relatively simple steps. The construction problem has now been automated (Bishop 1978).
Simple algebraic operations such as ![]() ,
, ![]() ,
, ![]() (for
(for ![]() a rational number),
a rational number), ![]() ,
, ![]() , and
, and ![]() can be performed using geometric constructions (Bold 1982, Courant and Robbins 1996). Other more complicated constructions, such as the solution of Apollonius' problem and the construction of inverse points can also accomplished.
can be performed using geometric constructions (Bold 1982, Courant and Robbins 1996). Other more complicated constructions, such as the solution of Apollonius' problem and the construction of inverse points can also accomplished.
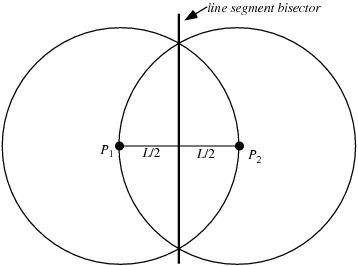
One of the simplest geometric constructions is the construction of a bisector of a line segment, illustrated above.
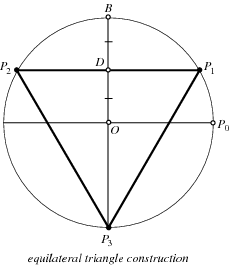 | 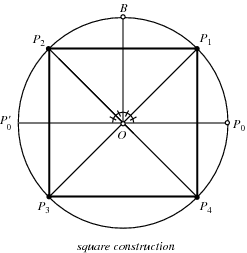 |
 | 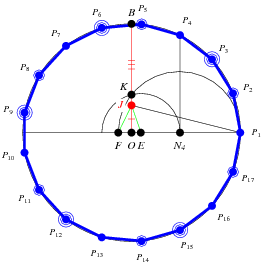 |
The Greeks were very adept at constructing polygons, but it took the genius of Gauss to mathematically determine which constructions were possible and which were not. As a result, Gauss determined that a series of polygons (the smallest of which has 17 sides; the heptadecagon) had constructions unknown to the Greeks. Gauss showed that the constructible polygons (several of which are illustrated above) were closely related to numbers called the Fermat primes.
Wernick (1982) gave a list of 139 sets of three located points from which a triangle was to be constructed. Of Wernick's original list of 139 problems, 20 had not yet been solved as of 1996 (Meyers 1996).
It is possible to construct rational numbers and Euclidean numbers using a straightedge and compass construction. In general, the term for a number that can be constructed using a compass and straightedge is a constructible number. Some irrational numbers, but no transcendental numbers, can be constructed.
It turns out that all constructions possible with a compass and straightedge can be done with a compass alone, as long as a line is considered constructed when its two endpoints are located. The reverse is also true, since Jacob Steiner showed that all constructions possible with straightedge and compass can be done using only a straightedge, as long as a fixed circle and its center (or two intersecting circles without their centers, or three nonintersecting circles) have been drawn beforehand. Such a construction is known as a Steiner construction.
Geometrography is a quantitative measure of the simplicity of a geometric construction. It reduces geometric constructions to five types of operations, and seeks to reduce the total number of operations (called the "simplicity") needed to effect a geometric construction.
Dixon (1991, pp. 34-51) gives approximate constructions for some figures (the heptagon and nonagon) and lengths (pi) which cannot be rigorously constructed. Ramanujan (1913-1914) and Olds (1963) give geometric constructions for ![]() . Gardner (1966, pp. 92-93) gives a geometric construction for
. Gardner (1966, pp. 92-93) gives a geometric construction for
Kochanski's approximate construction for ![]() yields Kochanski's approximation
yields Kochanski's approximation
Steinhaus (1999, p. 143). Constructions for ![]() are approximate (but inexact) forms of circle squaring.
are approximate (but inexact) forms of circle squaring.
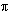 = 3.141592...)
= 3.141592...)
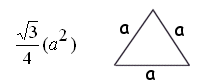
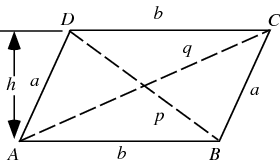
 [s(s-a)(s-b)(s-c)] when s = (a+b+c)/2
[s(s-a)(s-b)(s-c)] when s = (a+b+c)/2