Inequalities in Triangles

Vertical Angles

Definition: Angles AOC and angle BOD are a pair of vertical angles if rays OA and OB are opposite rays of the line AB and if rays OC and OD are opposite rays of line CD.

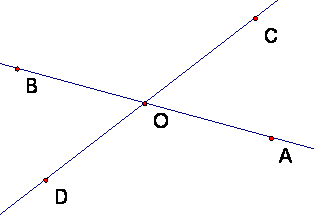
In other words, the two segments AB and CD intersect at O. When two lines intersect at a point O in this way, they form two pairs of vertical angles, AOC and BOD and BOC and AOD, as in the figure.

Theorem: If AOC and BOD are a pair of vertical angle, they are congruent.

Proof: This follows from observing that AOC and COB are supplementary (i.e, their sum is a straight angle), and also that COB and BOD are supplementary. See B&B, p. 52.

---

Exterior Angle Theorem

Definition of an exterior angle of a triangle

In triangle ABC, the interior angle at A (normally called just angle A), is the angle BAC.

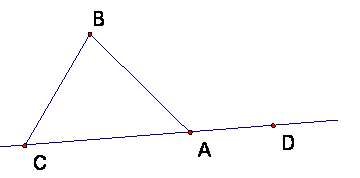
If D is any point on the opposite ray of AC, then DAB is an exterior angle of the triangle ABC at A. (There is a second exterior angle at A formed by extending side AB instead of side AC, the two exterior angles are a pair of vertical angles.)

Theorem: An exterior angle at A of triangle ABC is great than either of the (interior) angles B or C.

Proof: For the proof, construct this figure. M is the midpoint of AB and ME = CM (so M is also the midpoint of CE).

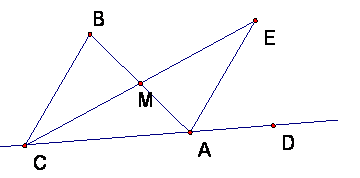
Then triangle MBC = triangle MAE by SAS, because

• angle CMB = angle EMA, by vertical angles
• MB = MA , since M is the midpoint of AB
• CM = EM, since M is the midpoint of CE

Consequently, by corresponding angles, angle MBC = angle MAE.

But angle MBC = angle B in the triangle.

Angle MAE <>

---

Greater Angle and Greater Side in a Triangle

Theorem: In a triangle ABC, side BC is greater than side CA, if and only if angle A (= angle CAB) is greater than angle B (= angle ABC).

In other words, greater sides are opposite greater angles.

Proof.

Part 1. First we prove one direction: greater sides imply greater opposite angles

Since BC > CA, then there is a point D on segment BC so that CD = CA.

• But this means triangle CAD is isosceles, so angle CAD = angle CDA.
• But angle CAD <>
• And angle CDA is an exterior angle at D of triangle ABD, so angle CDA > angle ABC.
• Together, this says angle CAB > angle CAD = angle CDA > angle ABC.

Part 2. Now we assume angle A is greater than angle B and prove that BC > CA.

This is accomplished by a bit of logical pigeonholing using Part 1.

If A is greater than B, we have three cases as possibilities

1. BC <>
2. BC = CA
3. BC > CA

Case 1, by Part 1 above, implies that angle B <>

Case 2 would imply that triangle ABC is isosceles with angle A = angle B, which again contradicts the hypothesis.

So Case 3 is the only possible case that can occur, and this proves Part 2.

Congruence Of Triangles

© Copyright 1997, Jim Loy

In Plane Geometry, two objects are congruent if all of their corresponding parts are congruent. In the first diagram, the two triangles have two sides which are congruent, and the angle between these sides is also congruent. Euclid proved that they are congruent triangles (Theorem I.4, called "Side-Angle-Side" of SAS). But, he was not happy with the proof, as he avoided similar proofs in other situations. The way he proved it, is to move one triangle until it is superimposed on the other triangle. Such a trick (superposition: placing one triangle on top of another, to see if they are congruent), is not considered legal, now. It involves some complicated assumptions. So, now this (SAS) is given as an assumption (postulate). It is the Side-Angle-Side Postulate.

Euclid proved his Side-Side-Side (SSS) Theorem (I.8) and his Angle-Side-Angle (ASA, diagram at the right) Theorem (I.26) in a similar way. In SSS, if a triangle has all three sides conguent to the corresponding sides of a second triangle, then they are congruent. In ASA, if a triangle has two angles and the side in between the angles congruent to the corresponding parts of a second triangle, then they are congruent. These too, are now assumed as postulates.

It is easy to construct a triangle given the lengths of the three sides (diagram on the left), or two sides and the included angle, or two angles and the included side. Given the ease of these constructions (especially SSS), it seems strange that the corresponding congruence "theorems" cannot be proven, except by slightly shady means (superposition).

All three of these congruence postulates are equivalent. You can assume any one of them, and prove the other two from there. See Congruence Of Triangles, Part II for a proof of this.

Euclid also proved an Angle-Angle-Side (AAS) as a corollary (a minor theorem derived directly from the parent theorem) to Theorem I.26. The situation SSA (or ASS) is not a theorem or postulate, as it is often ambiguous, there are often two different non-congruent triangles with two congruent sides and a congruent angle at the end of one of the sides.

---

Note: In the above, I used the term "congruent" instead of "equal" when comparing sides and angles. Numbers are equal. Line segments (sides) and angles are congruent. Calling them "equal" is a sloppy way of saying that their measures (lengths or sizes) are equal. Nevertheless, I do use this more informal terminology in some of my articles.

---

Addendum:

In answer to email about proving these congruence theorems/assumptions, I wrote this:

The issue is this (using SAS as an example). If you take your angle and two segments, and move it to somewhere else, does the triangle that you get, by drawing the third side of your moved object, change shape (is it congruent to the original triangle)? We can say that it doesn't change shape (that would seem to be right), but we can't prove it. Moving things is a complicated process; do we need postulates that say what changes and what does not change when we move a geometric figure? It is simpler to make congruence assumptions. Then we know that a triangle over here is congruent to a triangle over there. And motion never enters into it.